Application of Fixed Point in LabVIEW
What is a fixed-point number
As the name implies, the number that does not move at the decimal point in the operation is the fixed-point number. For fixed-point numbers, we define the total number of bits that it occupies and the position of the decimal point. The data range and data accuracy that can be expressed by fixed-point numbers in different formats will also vary.
Such a specification is usually used to express fixed-point numbers. Where s represents a sign bit, m represents a word length, and n represents an entire digit length. The fixed-point storage space in LabVIEW, the maximum limit is 64bit.
Figure: Signed fixed point representation
For example, an unsigned fixed-point number with a word length of 8 and an integer number of 4 is represented by <+, 8, 4>. The range is from 0 to 15.9375 and the increment value is 0.0625.
Figure: LabVIEW Instant Help for Fixed-Point Functions
Why choose fixed point?
[High efficiency, occupy less resources]
In general, fixed-point operations are simpler and more efficient in computers; floating-point operations are more complex and relatively inefficient in computers.
Figure: Fixed-point and single-precision floating-point numbers plus multiplication operations occupy resources
[short execution time]
Fixed-point operations can be performed in a single-cycle Timed Loop (SCTL) on the FPGA, but compilation fails if you want to perform floating-point operations in a single-cycle Timed Loop.
Calculation of the max, min and delta of fixed point
The max and min of the fixed-point number are determined by the sign bit, the word length and the integer length, but the delta size has nothing to do with the sign bit.
We define a fixed-point number as <+, m, n>. When all m words have a length of 1, the value has a maximum value; when all m words have a length of 0, the value is the smallest value. value.
Figure: Unsigned fixed-point delta representation
The maximum value of an unsigned fixed-point number is , the minimum value is 0, and the delta value is
. Similarly, for a signed fixed-point number, the sign bit is 0, and all other bits are 1 and take the maximum value; the sign bit is 1 and all other bits are 0. At this time, the minimum value is taken; the increment value is Delta. Still for
.
Fixed-point operations
ã€addition】
When adding fixed-point numbers, add <+, m, n> and <+, m, n>, and use <+, m+1, n+1> to fully include all possible results. . That is, the number of digits in the fractional part does not change. Since the integer may carry, the number of digits in the integer part is increased by one, and the length of the digit is also increased by one.
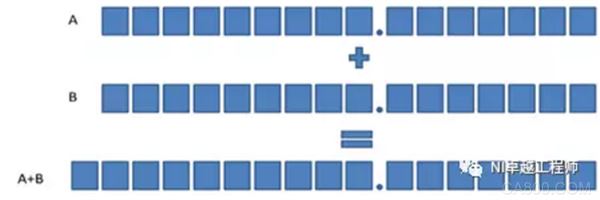
Figure: Addition of two unsigned fixed-point numbers with the same configuration
If the fixed node number configuration at both ends of the Add node is different, the fractional part number is taken as the larger value between A and B, the integer part number is taken as the larger value between A and B and +1, and the word length is equal to the sum of the fractional number and the integer number of digits. .
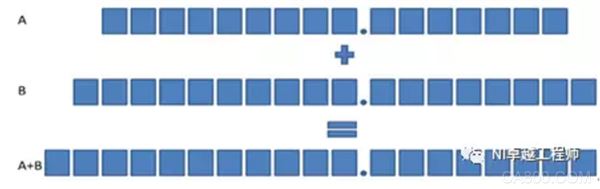
Figure: Addition of unsigned fixed-point numbers for two different configurations
Subtraction
Regardless of whether or not the subtrahend and the subtraction are signed, the result must be a signed fixed-point number. That is, the fixed points in the two configurations <+, m, n> are subtracted. The result is <±, m+1, n+1>. Of course, the two configurations are subtracted from the fixed point of <±, m, n>. It is still <±, m+1, n+1>.

Figure: Subtraction of fixed-point numbers
ã€multiplication】
The multiplication rule for fixed-point numbers is that <+, m, n> is multiplied with <+, a, b> and the result is <+, m+a, n+b>.
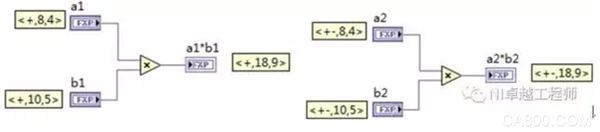
Figure: Multiplication of fixed-point numbers
ã€division】
The dividend is the maximum value, and when the integer part of the divisor is all 0 and the fraction part is 0....01, the result with the largest integer part can be obtained. The result is:
The integer part of this result is n+ab.
In summary, the maximum number of integers in the result is n+ab, the maximum number of fractional parts is m-n+b, and the word length is the sum of the two. Therefore, the expression of the large result of dividing <+, m, n> and <+, a, b> is <+, m+a, n+ab>.
Similarly, divide two signed fixed-point numbers <±, m, n> and <±, a, b> and the results are expressed as <±, m+a+1, n+a-b+1>. .

Figure: Division of fixed-point numbers
Fixed point overflow and rounding?
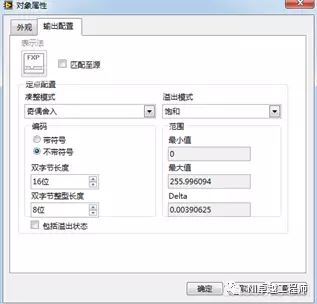
Figure: Fixed point overflow and rounding settings
ã€overflow】
When the value resulting from the fixed-point number operation exceeds the range we have configured, overflow will occur. There are two kinds of overflow modes for fixed-point operations: Saturate mode and Wrap mode.
Saturation - If the output value is greater than the maximum acceptable value of the output type, LabVIEW forces the value to be rounded to the specified maximum value. If the value is less than the minimum value of the acceptable range, LabVIEW casts the value to the specified minimum value.
Wrap-around - If the output value is outside the acceptable range of the output type, LabVIEW discards the valid bits of the output value until the output value is within the acceptable range of the output type. This option requires that the output value conforms to the specified encoding method. If you select this option, you cannot specify an acceptable range because LabVIEW automatically adapts the range to encoding.
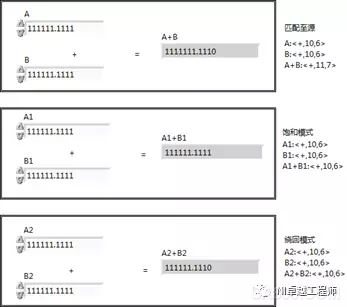
Figure: Fixed point overflow
Complete a numerical comparison in saturation mode. This is why choosing saturation mode will take up additional resources for the FPGA. For this reason, operation in saturated mode will reduce the maximum clock rate. However, it is not difficult to see that calculations in saturated mode can often obtain more accurate results.
[Completely]
Rounding occurs when the precision of the input value or operation result is greater than the precision of the output type. This situation occurs more often with operations such as division, reciprocal, and square root.
Truncate - Rounds down to the nearest value that the output type can represent. LabVIEW will discard the least significant bit of this value. The rounding mode has the best performance, but the output value obtained has the lowest accuracy.
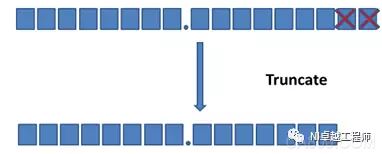
Figure: Truncation rounding
Round-Half-Up Rounds to the nearest value that the output type can represent. If the value is between two valid values, the pattern rounds the value to the larger of the two valid values. LabVIEW adds half the least significant bit to the output value and then truncates the value. This rounding mode is more accurate than the output value of the truncated mode but has a greater impact on performance.
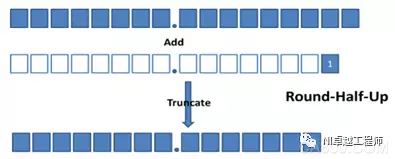
Figure: Half Value Up
Round-Half-Even - Rounded to the nearest value that the output type can represent. If the rounded value is exactly between two valid values, LabVIEW checks the bit in the value that will be the least significant bit after rounding. If this bit is 0, the pattern will round the value to the smaller value that the output type can represent. If this bit is not 0, the pattern rounds the value to the larger of the two valid values. This rounding mode has the greatest impact on performance, but its output value is more accurate than truncation mode. This mode also tends to tend towards larger values ​​after neutralization has performed multiple half-value up roundings. This mode is the default rounding mode.
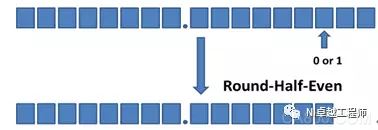
Figure: Odd and even rounding
Truncation rounding is the most efficient mode, but it is often not the best accuracy. Compared with the half-value up mode and the parity rounding mode, the accuracy of the two can be said to be quite the same, but the parity rounding mode can effectively avoid the results that multiple rounding may bring results tend to be more worthwhile. This mode is also LabVIEW. The default rounding mode.
For more information, please visit the official website of NI:
Http://
- The Description of PCB/FPC/Ceramic Antenna
Cellular /WiFi multi-band embedded flexible PCB antenna
It is equivalent to pulling out the antenna line on the PCB board and using other external metals to do the antenna. It is usually used in medium and low end mobile phones with complex frequency band and smart hardware products.
Advantages: suitable for almost all small electronic products, can do more than ten frequency band of complex antennas, good performance, low cost.
Disadvantages: need to be debugged separately for each product.
The Picture of PCB/FPC/Ceramic Antenna

pcb antenna,5g pcb antenna,lte pcb antenna,lte pcb antenna,2.4g pcb antenna
Yetnorson Antenna Co., Ltd. , https://www.yetnorson.com